Summary Of My Olympic Gold Medal Prediction
I decided to approach this competition mainly using statistical knowledge that I was already familiar with. Currently being a second year university maths student I wanted to take the techniques I have learned these past couple years and use them in a practical sense. I thought this would be an interesting method to use in order to see how well my knowledge would predict the gold medal table in Paris compared to more complex procedures other entries may offer. However, I did push myself by looking ahead to future studies by researching techniques such as k-means clustering to make data handling more manageable using Cui et al. (2020).
Where I Started
The scoring of this competition was intriguing to me. The fact that all correct placements of countries are weighted the same meant that it was important to take into consideration all competing nations. In doing so I collected open data from https://www.wikipedia.org/ taking the gold medal count for each nation for the past 11 Olympic games. From looking at these medal tables I decided to not take data from any earlier Olympics due to the fact it included many former nations as well as it did not accurately represent what the games are today.
When I was formulating my data at the start of my research I was aware of the range in countries winning a gold medal each Olympic games. I thought that it would be interesting to model this trend using linear regression to see if my overall prediction is similar to a statistical model. Using variables such as Ev to denote the number of events, Nat to denote the number of nations at a particular games alongside time, I found that I have predicted 71 countries to earn a gold medal this year. The result I achieved from adding these variables was exciting as all my residuals were very small with each predicted value being 0 or 1 at most away from the true value. In my final prediction I did generate less than 71, however I do believe that it is likely that the number of countries winning a gold medal will increase from Tokyo. The influence of social media on exposing more people to an event, improved female participation as well as the increased funding into sport around the world are just a few reasons for this.
Countries_With_Medal <- data.frame(
X = 1:7,
Ev = c(300,301,302,302,306,339,329), #events
Nat = c(199,201,204,206,207,206,206), #nations
Y = c(52,56,55,55,59,65, rep(NA, 1))
)
model_Countries_With_Medal <- lm(formula = Y ~ X + Nat + Ev, data = Countries_With_Medal)
predict(object = model_Countries_With_Medal, newdata = Countries_With_Medal) 1 2 3 4 5 6 7
53.17309 54.67044 54.25913 55.79669 59.08205 65.01861 70.77559 K-means Clustering
Throughout this competition I wanted to push my understanding of statistics, hence the use of k-means clustering. This technique allowed me to find groups of countries that share similar medal counts. I wanted to use this to break down my prediction into smaller more manageable problems that I could analyse in more detail. After several attempts of clustering in R, I found that taking a larger dataset of Olympic data formed results that I didn’t feel accurately depicted the outcome in Paris. For this reason I instead shortened the data I used to the past 4 Olympic games to give a better representation of how countries will actually perform this year.
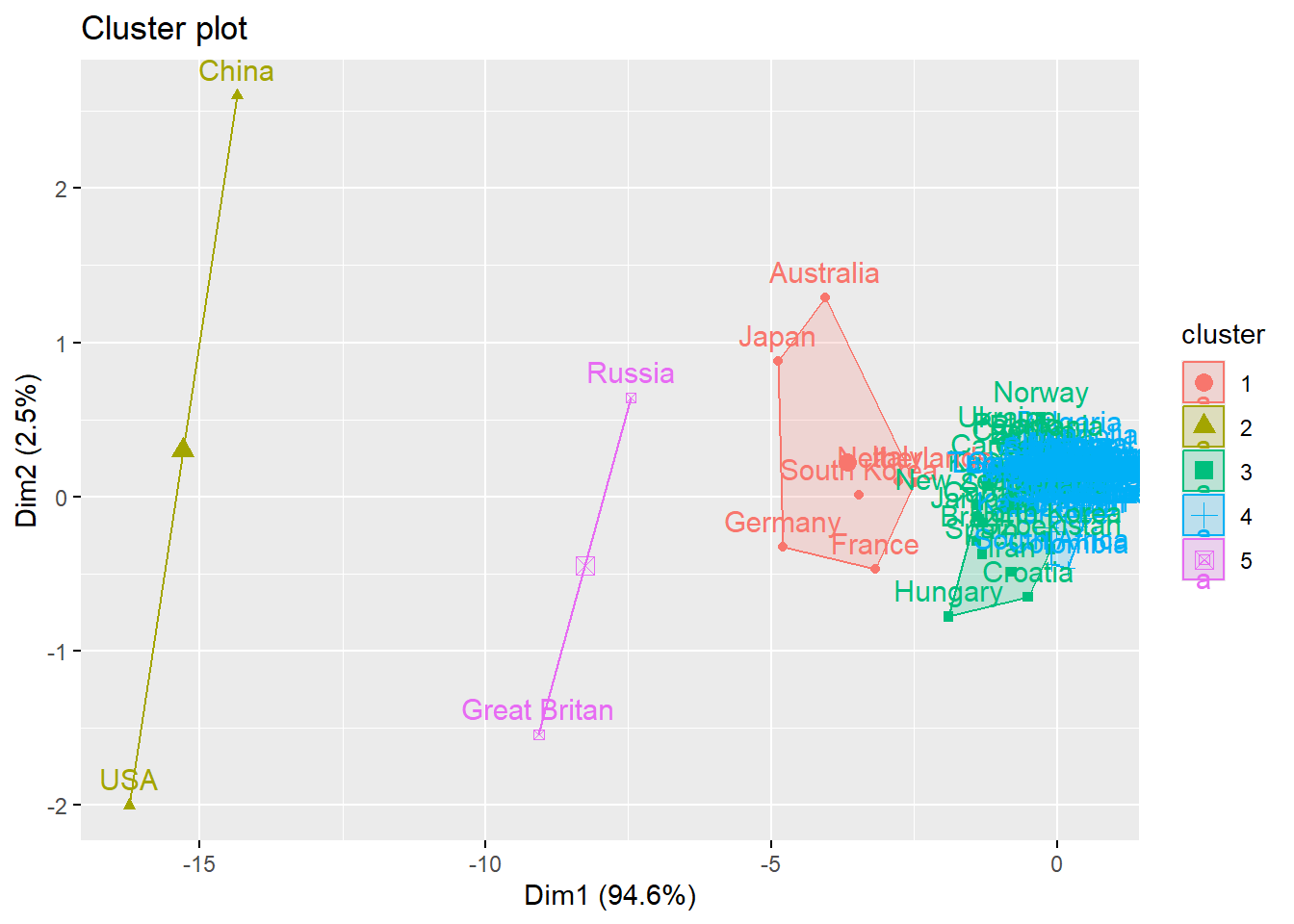
My analysis for k-means clustering was taken using the Kassambara and Mundt (2020) package to create and visualize my clusters.
In the end I opted for 5 clusters (found using the elbow method) to show the spread in my data. These 5 clusters which formed were generally what I expected to see, ranging from the highest gold medal count countries in one cluster to the countries who mostly earn 0 or 1 in a particular Olympic games in another. From there I decided to look at every cluster individually as I was quite happy with the fact that they gave the rough positions of each country. For example, I believed that the cluster containing the USA and China will always place above the cluster of Japan, Australia etc. Because of this I was interested instead in the placements of countries within its respective cluster, as I felt that within a cluster different factors would affect a country’s position.
Linear Models
This year I have focused mainly on linear models and therefore I wanted to incorporate this into my competition entry. Taking cluster 3 which consisted of 7 countries I first considered each country separately and created a linear model to predict how many gold medals they could earn in Paris. Then I compared the totals to see who would place higher in the table. But, to try an alternative more practical method I decided to next create a larger model which took all countries in a certain cluster into one equation. This was very useful for the larger clusters where doing each country individually would have been time consuming.
Factors such as host nation, GDP and number of athletes a nation takes in my opinion will affect the total gold medal count for a country. I introduced the variable of the host nation (0 for not the host,1 for the host) because I believe in home advantage. To find evidence in this I plotted graphs taking all host countries since Sydney 2000 and graphed how many gold medals they won each Olympic Games. It was clear to see that the majority of these nations peaked at home. This could be due to factors such as athlete participation in each event, crowd support as well as more money being funded into the athletes in order to produce better results at home. Furthermore I was confident in suggesting that France will continue this trend and have a higher gold medal count than usual.
Call:
lm(formula = cluster_4$Number_Of_Golds ~ cluster_4$Number_Of_Events +
cluster_4$Number_Of_Athletes + cluster_4$Host + cluster_4$GDP +
cluster_4$Previous_Gold + cluster_4$Previous_2_Gold)
Residuals:
Min 1Q Median 3Q Max
-3.5924 -1.4062 -0.2321 1.3618 7.1253
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.6558133 4.0396002 -0.657 0.51216
cluster_4$Number_Of_Events 0.0122221 0.0130548 0.936 0.35105
cluster_4$Number_Of_Athletes 0.0087146 0.0034205 2.548 0.01212 *
cluster_4$Host 2.0756713 2.1371182 0.971 0.33339
cluster_4$GDP -0.0007990 0.0005821 -1.372 0.17249
cluster_4$Previous_Gold 0.2711416 0.0808126 3.355 0.00106 **
cluster_4$Previous_2_Gold 0.1363718 0.0717962 1.899 0.05993 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.991 on 119 degrees of freedom
(21 observations deleted due to missingness)
Multiple R-squared: 0.3296, Adjusted R-squared: 0.2958
F-statistic: 9.751 on 6 and 119 DF, p-value: 1.003e-08I found it very interesting to see that the number of athletes and previous gold medal count were the most significant in my combined model. This is perhaps because many athletes may return for another Olympics and look to find success in the same event. Hence, the most recent achievements will be a useful indicator for total gold medal count. Secondly it suggests the more competitors a country entered the higher chance of earning a medal at the Olympics.
I was aware that my linear regression had some setbacks such as I obtained a few negative values as well as it didn’t give count data as a result. However, as a basis for predicting a rough gold medal count I was happy to use this simple model.
More Than Statistics?
When making my overall gold medal table I chose not to rely just on my statistical data, instead use it as a basis to refer to. Sport includes many factors that are hard to measure such as how an athlete will perform on the day. Because of that I wanted to add some personal ‘gut feeling’ tweaks to my submission.
One example of this is that I believe that having an ‘inside knowledge’ on sports played at the Olympics is very useful when allocating overall position. Outside of mathematics one of my major passions is athletics. For this reason when looking at my data I saw that some countries have only ever won gold medals in athletics and I used my judgement to say if they could replicate the same results in Paris. My only concern is that I could have introduced bias to any favourite athletes I may have (ie/ the 3000m steeplechase Moroccan, El Bakkali) but I wanted to take some risk using my knowledge of the sport.